Prerequisites

Scalar Product

Consider u,v∈Rd.

The scalar product <u;v> (sometimes written also as u.v) is

<u;v>=d∑i=1uivi

<u;v> is

• Symmetric. <u;v>=<v;u>
• Bilinear.

  <λu+μu';v>=λu;v+μ<u';v>
  u,v,u'∈Rd
  λ,μ∈R

• <z;z>=∥z∥2

Cauchy-Schwarz Inequality

Consider non-zero x,y∈Rn. The absolute value of the dot product;

|<x,y>|≤∥x∥∥y∥

or

|x.y|≤∥x∥∥y∥

the value is equal when x, y are colinear.

Let p(t)=∥ty−x∥2≥0

This value is positive as ∥z∥=√z21+⋯+z2m≥0. Also note by definition of scalar product that ∥z∥=z.z

Hence,

Let p(t)=(ty−x).(ty−x)≥0

using distributive property of dot product

p(t)=ty.ty−x.ty−ty.x+x.x≥0

p(t)=t2(y.y)−2(x.y)t+x.x≥0

if we define;

y.y=a

−2(x.y)=b

x.x=c

then we obtain

p(t)=t2(a)−2(b)t+c≥0

for t=b2a,

p(b2a)=(b24a2)(a)−2(b)(b2a)+c≥0

b24a−b22a+c≥0

−b24a+c≥0

c≥b24a

Hence

4ac≥b2

Therefore, substituting

4(y.y)(x.x)≥[−2(x.y)]2

4∥y∥2∥x∥2≥4(x.y)2

∥y∥2∥x∥2≥(x.y)2

∥y∥∥x∥≥(x.y)

Consider the colinear case if x=cy

| cy.y |	=c | y.y |
	=c∥y∥2
	=c∥y∥∥y∥
	=∥cy∥∥y∥
	=∥x∥∥y∥

Intermediate Value Theorem

Suppose f is a function continuous in every point in the interval [a,b];

• f will take on every value between f(a) and f(b) over the interval.
• for any value L between the value of f(a) and f(b), ∃c in [a,b] for which f(c)=L

Mean Value Theorem

For f continuous in [a,b] and differentiable over (a,b), ∃c where the instantaneous change is equal to the average change.

hence ∃x such that

f′(x)=f(b)−f(a)b−a

or

f′(x)(b−a)=f(b)−f(a)

Fixed Point Iteration

In solving f(x)=0, we rewrite as x=g(x).

Note This is always possible; f(x)=0

f(x)+x=x g(x)=x

The root r=g(r) where r is a fixed point. Hence with initial guess x0 compute root g(x0). Idea is that x1=g(x0) will be closer to r.

• choose x0
• xk+1=g(xk). Iterate until stop criteria are met.

Convergence Analysis

Let r be a root such that r=g(r). The value of x at iteration step k, xk+1=g(xk).

• The error at step k = & |xk−r|
• The error at step k+1 = & |xk+1−r|=|g(xk)−g(r)|

Considering that the error at step k+1=|g(xk)−g(r)| Using the mean value theorem, there exists point ξ such that,

|g(xk)−g(r)|=|g′(ξ)(xk−r)|

where ξ∈[xk,r]

Note that at each iteration the error xk−r is multiplied by |g′(ξ)|. Therefore,

• if |g′(ξ)|<1 & ek+1<ek & → Convergence
• if |g′(ξ)|>1 & ek+1>ek & → Divergence

Convergence Condition ∃ I=[r−c,r+c] for some c>0 such that |g′(x)|<1 on I and xo∈I

Graphical Approach

Setting y=x and y=g(x), the intersection is the solution as x=g(x)

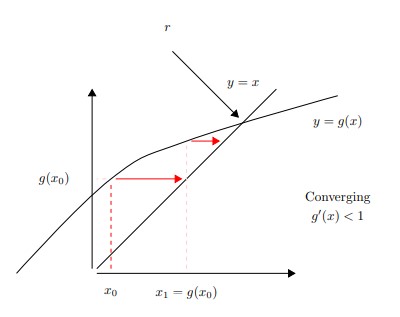
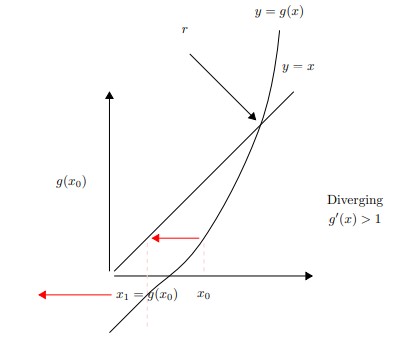
Example

Solve f(x)=x−cos(x)=0

Solution x=g(x)=cos(x)

Solving to 4 point accuracy, selecting initial guess of x0=1

x1=	cos(x0)=cos(1)=	0.5403
x2=	cos(0.5403)=	0.8576
x3=	cos(0.8576)=	0.6543
	…
x23=		0.7390
x24=		0.7391

Therefore r≈0.7391→ Convergent