Prerequisites

Scalar Product

Consider $\textbf{u}, \textbf{v} \in {R}^d$.

The scalar product $<\textbf{u};\textbf{v}>$ (sometimes written also as $\textbf{u} . \textbf{v}$) is

$$<\textbf{u};\textbf{v}> = \sum_{i=1}^{d} u_i v_i$$

$<\textbf{u};\textbf{v}>$ is

• Symmetric. $ <\textbf{u};\textbf{v}> =<\textbf{v};\textbf{u}> $
• Bilinear.

  $<\lambda\textbf{u} + \mu\textbf{u'};\textbf{v}> = \lambda{\textbf{u};\textbf{v}} + \mu<\textbf{u'};\textbf{v}>$
  $\textbf{u}, \textbf{v} , \textbf{u'} \in {R}^{d}$
  $\lambda, \mu \in {R}$

• $<\textbf{z};\textbf{z}> = \parallel \textbf{z} \parallel^{2}$

Cauchy-Schwarz Inequality

Consider non-zero $\textbf{x},\textbf{y} \in {R}^n$. The absolute value of the dot product;

$$|<\textbf{x},\textbf{y}>| \leq \parallel\textbf{x}\parallel \parallel\textbf{y}\parallel$$

or

$$|\textbf{x}.\textbf{y}| \leq \parallel\textbf{x}\parallel \parallel\textbf{y}\parallel$$

the value is equal when $\textbf{x}$, $\textbf{y}$ are colinear.

Let $$p(t) = \parallel t\textbf{y} -\textbf{x}\parallel^2 \geq 0$$

This value is positive as $\parallel z\parallel=\sqrt{z_1^2+\dots+z_m^2} \geq 0$. Also note by definition of scalar product that $\parallel z\parallel = z.z $

Hence,

Let $$p(t) = (t\textbf{y} -\textbf{x}).(t\textbf{y} -\textbf{x})\geq 0$$

using distributive property of dot product

$$p(t) = t\textbf{y}.t\textbf{y} -\textbf{x}.t\textbf{y} -t\textbf{y}.\textbf{x} + \textbf{x}.\textbf{x}\geq 0$$

$$p(t) = t^2(\textbf{y}.\textbf{y}) -2(\textbf{x}.\textbf{y})t + \textbf{x}.\textbf{x}\geq 0$$

if we define;

$$\textbf{y}.\textbf{y} = a$$

$$-2(\textbf{x}.\textbf{y}) = b$$

$$\textbf{x}.\textbf{x}=c$$

then we obtain

$$p(t) = t^2(a) -2(b)t + c \geq 0$$

for $t=\frac{b}{2a}$,

$$p \left(\frac{b}{2a} \right) = \left(\frac{b^2}{4a^2}\right)(a) -2(b)\left(\frac{b}{2a}\right) + c \geq 0$$

$$\frac{b^2}{4a}-\frac{b^2}{2a}+c \geq 0$$

$$-\frac{b^2}{4a}+c \geq 0$$

$$c \geq \frac{b^2}{4a}$$

Hence

$$4ac \geq b^2$$

Therefore, substituting

$$4(\textbf{y}.\textbf{y})(\textbf{x}.\textbf{x}) \geq [-2(\textbf{x}.\textbf{y})]^2$$

$$4 \parallel\textbf{y}\parallel^2 \parallel\textbf{x}\parallel^2 \geq 4 (\textbf{x}.\textbf{y})^2$$

$$\parallel\textbf{y}\parallel^2 \parallel\textbf{x}\parallel^2 \geq (\textbf{x}.\textbf{y})^2$$

$$\parallel\textbf{y}\parallel \parallel\textbf{x}\parallel \geq (\textbf{x}.\textbf{y})$$

Consider the colinear case if $\textbf{x}=c\textbf{y}$

| $c\textbf{y}.\textbf{y}$ |	$= c$ | $\textbf{y}.\textbf{y}$ |
	$ = c\parallel\textbf{y}\parallel^2$
	$ = c\parallel\textbf{y}\parallel \parallel\textbf{y}\parallel$
	$ = \parallel c \textbf{y}\parallel \parallel\textbf{y}\parallel$
	$ = \parallel\textbf{x}\parallel \parallel\textbf{y}\parallel$

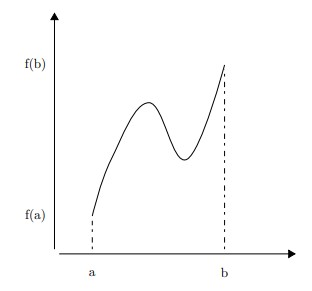
Intermediate Value Theorem

Suppose $f$ is a function continuous in every point in the interval $[a,b]$;

• $f$ will take on every value between $f(a)$ and $f(b)$ over the interval.
• for any value $L$ between the value of $f(a)$ and $f(b)$, $\exists c$ in $[a,b]$ for which $f(c)=L$

Mean Value Theorem

For $f$ continuous in $[a,b]$ and differentiable over $(a,b)$, $\exists c$ where the instantaneous change is equal to the average change.

hence $\exists x$ such that

$$f'(x) = \frac{f(b)-f(a)}{b-a}$$

or

$$f'(x)(b-a) = f(b) - f(a)$$

Fixed Point Iteration

In solving $f(x) =0$, we rewrite as $x=g(x)$.

Note This is always possible; $$f(x)=0$$ $$f(x)+x=x$$ $$g(x)=x$$

The root $r=g(r)$ where r is a fixed point. Hence with initial guess $x_0$ compute root $g(x_0)$. Idea is that $x_1=g(x_0)$ will be closer to $r$.

• choose $x_0$
• $x_{k+1}=g(x_k)$. Iterate until stop criteria are met.

Convergence Analysis

Let $r$ be a root such that $r=g(r)$. The value of $x$ at iteration step $k$, $x_{k+1}=g(x_k)$.

• The error at step $k$ = & $|x_k - r|$
• The error at step $k+1$ = & $|x_{k+1} - r| = |g(x_k) - g(r)|$

Considering that the error at step $k+1 = |g(x_k) - g(r)|$ Using the mean value theorem, there exists point $\xi$ such that,

$$|g(x_k) - g(r)| = |g'(\xi)(x_k - r)|$$

where $\xi \in [x_k, r]$

Note that at each iteration the error $x_k - r$ is multiplied by $|g'(\xi)|$. Therefore,

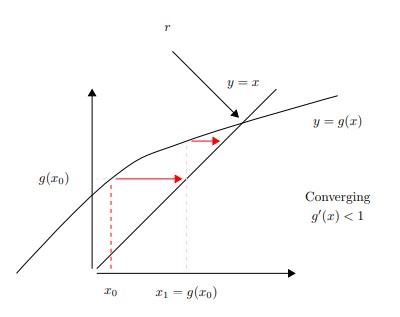
• if $|g'(\xi)|<1$ & $e_{k+1} < e_k$ & $\rightarrow$ Convergence
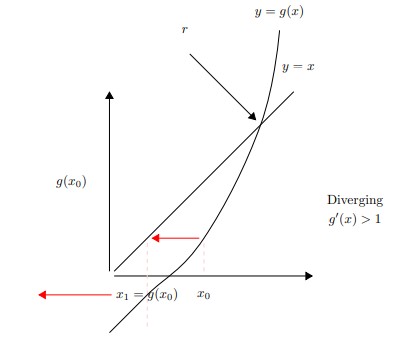
• if $|g'(\xi)|>1$ & $e_{k+1} > e_k$ & $\rightarrow$ Divergence

Convergence Condition $\exists$ $I=[r-c, r+c]$ for some $c>0$ such that $|g'(x)|<1$ on $I$ and $x_o \in I$

Graphical Approach

Setting $y = x$ and $y = g(x)$, the intersection is the solution as $x=g(x)$

Example

Solve $f(x)= x-cos(x) = 0$

Solution $x=g(x)=cos(x)$

Solving to 4 point accuracy, selecting initial guess of $x_0=1$

$x_1=$	$cos(x_0)= cos(1)=$	0.5403
$x_2=$	$cos(0.5403)=$	0.8576
$x_3=$	$cos(0.8576)=$	0.6543
	…
$x_23=$		0.7390
$x_24=$		0.7391

Therefore $r \approx 0.7391 \rightarrow$ Convergent